Reply to Hubert Goenner
A response to Hubert Goenner’s review of
Kinematics: The Lost Origins of Einstein’s Relativity,
in the journal Isis, vol. 101, No. 3 (2010), pp. 633-635.
Alberto A. Martínez
To start, Hubert Goenner complains that my “reconstruction of Einstein’s path to special relativity in the sixth chapter relies almost entirely on secondary and tertiary sources. While Martínez is careful to point this out with regard to his quotations, he nevertheless uses this method, which is not well respected in the history of science.” Goenner then contrasts my book with Albrecht Fölsing’s 1993 biography of Einstein, as if Fölsing had better recognized the historiographic constraints of the matter. I appreciate Fölsing’s work as outstanding, I strongly recommend his book, yet I have to say that neither Fölsing, nor any other account of Einstein’s path to special relativity, handles documentary evidence more accurately and comprehensively than my book. Like other writers, Fölsing makes many speculations (“he must have,” “he should have,” “probably,” “unlikely,” etc.), some mistakes (e.g., that the name “relativity principle” first appeared in Poincaré’s writings, that Einstein pointed to clock towers when talking with Besso, etc.), and plenty of hagiography (“genius,” “brilliant,” “genius,” “unprecedented,” “genius, ”etc.). By contrast, a goal for Kinematics was to systematically avoid speculations and hagiography, and to focus instead on evidence. For the record, listing only writers and dates, Fölsing cited the following sources, having at least some indirect relevance for tracing Einstein’s path to relativity:
Abraham 1903, 1904; Besso 1952; Byland 1928; Cohen 1955; Drude 1894; Einstein 1895, 1898, 1899 (4), 1901 (5), 1902, 1903 (2), 1904, 1905 (2), 1912, 1917, 1919, 1920, 1921, 1922, 1924, 1932, 1946, 1952 (5), 1955 (2); Fluckiger 1974; Föppl 1894; Frank, 1949; Genewin 1924; Helmholtz 1895; Hertz 1890, 1892, 1895, 1899; Humboldt, 1845, Kant 1781, 1786; Kaufmann 1902; Kirchhoff 1897; Kollros 1955; Lorentz 1895, 1904; Mach 1883; Maric 1900; N.G. Bern 1903; Sauter 1901, 1955; Shankland 1963; Pais 1982; Poincaré 1898, 1900, 1902, 1904, 1905; Reiser 1930; Solovine 1956, Talmey 1932, Voigt 1877; Wertheimer 1916/1945; Wien, 1904 (2); Winteler-Einstein 1924.
Clearly, Fölsing used many retrospective sources (“secondary and tertiary” as Goenner calls them) in addition to sources that predate June of 1905. By comparison, the sources I cited for the same purpose are:
Abraham 1903, 1904; Ampère 1834, Besso, 1947, 1952; Boltzmann 1897, 1899, 1900; 1952; Bernstein 1869; Bota 1898; Bucherer 1904; Byland 1928; Cohen 1955; Cohn 1904; Dedekind 1887; Drude 1894; Einstein 1895, 1896, 1898, 1899 (3), 1900, 1901 (7), 1902 (3), 1903, 1904 (4), 1905 (2), 1906, 1907 (3), 1910, 1911 (3), 1912 (3), 1912-14 ms., 1914, 1915 (2), 1916, 1917 (2), 1918, 1920 (2), 1921 (3), 1922 (3), 1924, 1926, 1927, 1929, 1930, 1932, 1934 (2), 1938, 1930s n.d., 1942, 1944 (2), 1946, 1948, 1952 (9), 1953 (2), 1954, 1955 (3); Ehrat 1952; Fluckiger 1974; Föppl 1894, 1898/1900; Forsee 1963; Franck 1952; Frank, 1949; Genewin 1924; Graf 2001, F. Habicht 1943; Heine 1881, Helmholtz 1866, 1870, 1878, 1887; Hentschel and Grasshoff 2005, Hoffmann 1982; Hertz 1884, 1890, 1894, 1895; Hume 1739; Infeld 1950; Kant 1758, 1770, 1781, 1783; Kaufmann 1902; Kirchhoff 1876/1883/1897; Koch ca.1986; Kollros 1952, 1955; Kornitzer 1951; Leich 1957; Lorentz 1882, 1886, 1895, 1900, 1901, 1902, 1904; Mach 1868, 1882, 1883/89, 1886; Marianoff 1944; Maric 1900, 1901 (3), 1903; Maxwell 1873; Michelmore 1963; Mill 1872; Minkowski 1898/1899; Moszkowski 1921; N.G. Bern 1903; Niewenhuis-von Uexküll 1953/1954; Niggli 1952; Ostwald 1893; Pais 1982; Pearson 1892; Piaget 1946; Poincaré 1897, 1898, 1889, 1900, 1902, 1904, 1905 (2), 1906; Reichinstein 1935; Reiser 1930; Riemann 1854; Ries 1904; Sauter 1901, 1955; Schopenhauer 1813, 1844, 1851; Seelig 1952, 1956; Shankland 1963, 1973; Solovine 1903, 1952, 1956; Spieker 1890; Spinoza 1677; Talmey, 1929, 1932; Tucci 1947; Vallentin 1954; Violle, 1892; Voigt, 1877; Wertheimer 1916/1945; P. Winteler 1952; Winteler-Einstein, 1924.
I did use more retrospective sources than Fölsing, but I also used more sources prior to 1905. Actually, I used more than twice as many relevant sources than any previous work on the roots of Einstein’s special relativity. Moreover, the important point, when writing history, is just that retrospective accounts should be handled carefully, not that they must be dismissed. After all, Einstein and company were not criminals conspiring to hide petty truths. For example, if someone, such as Einstein’s good friend Jakob Ehrat, wrote to Einstein’s trusted biographer, Carl Seelig, reporting that Einstein once told him that his key idea of the relativity of simultaneity first came to him early one morning as he was getting up from bed, then why should we omit that? Even Einstein read that account and accepted it, and his coworker Banesh Hoffman independently once reported that Einstein told him the same thing, and, this is entirely consistent with other retrospective accounts. What I did was to bring together nearly all of these accounts.
Goenner has not contributed to the history of special relativity, so he does not appreciate how Kinematics contributes to the field. To clarify the matter, let me echo the description of the field as summarized by John Stachel (in 1989), who has contributed richly to it. Stachel remarked on the dearth of manuscript sources on Einstein’s ruminations prior to 1905, and he argued that therefore the best we can do is to carefully take account of the varied extant evidence, prior and posterior to 1905, and “construct a plausible conjecture,” based on methodological hypotheses. Accordingly, Stachel, Fölsing, Arthur I. Miller, and many other writers, proceeded to do just that that. That has all been fine and it has been very helpful. Yet by contrast, what distinguishes Kinematics from other works is that I tried to keep conjectures to a very minimum and to focus instead on collecting and conveying neglected evidence. Thus, whereas Fölsing, for example, only very briefly alluded to the fact that, prior to 1905, Einstein tried to formulate a theory in which the speed of light depends on its source, and Fölsing cited only one letter to that effect, my book instead clearly describes this phase of Einstein’s trajectory, on the basis of no less than 12 sources: 5 letters by Einstein, 3 interviews, 1 manuscript, 1 passage in his book, and 2 books he had read. Clearly, the more sources we use, the less we need to fill gaps with conjectures, and that was my aim: to provide an account thick on evidence and thin on conjectures.
Moving on, Goenner claims that my arguments (in Chapter 8) about ambiguities between scalar and vector quantities, such as speed and velocity, disappear “if one of the coordinate axes is made coincident with the direction of the relative velocity of inertial reference systems…” What he claims is nothing new, it is a basic and common assumption when deriving Lorentz transformations. But to the contrary, my point was precisely that operations with positive and negative numbers often do not capture physical vectorial distinctions, such as speed and velocity, because arithmetic and “Cartesian” coordinates make no distinction between, for example, 5 and +5. This was recognized by leading contributors to the foundations of mathematics such as William Rowan Hamilton and Bertrand Russell. This lack of distinction is systematically disregarded in derivations of Lorentz transformations, so that writers claim, for example, that speed multiplied by duration produces a coordinate (positive or negative), that is, a displacement, whereas according to the rules of vectors, they should produce a distance (a signless magnitude).
Regardless, Goenner disregards the 24 pages of explanation that I gave on this point, and complains that my claim that “ordinary vector algebra could not be used to derive relativity theory” is wrong. Perhaps Goenner is right, I would be glad to see such a derivation, but whenever I had analyzed derivations that purport to do just that, I found that they are defective. Therefore, I sent him an email:
Dear Professor Goenner,
Thank you for taking the time to review my book for Isis. I was disappointed that the review is rather negative, especially inasmuch as it scarcely points out its actual contributions. I will write a reply and would there like to explain the vectorial issue about deriving the LT. To that end, I’m hoping that you can please point me to a published derivation that begins from and fully employs, specifically, the three dimensional vector algebra formulated by Heaviside and Gibbs in the 1890s and elucidated by E.B. Wilson. Rather than having me choose a particular past derivation and point out defects, which might seem selective, I’d rather use a derivation that you have selected as good, so that I’m replying directly that.
After some time, professor Goenner did cordially reply to my message, and I thank him for that. But still, he did not give an example as I had requested and he did not expand on his claim about vectors. (Update: Goenner replied again, see below.) Therefore, to clarify this issue I myself have to choose a particular derivation to illustrate my point. A classic, meticulous, and authoritative book is The Theory of Relativity, by Christian Møller. There, for example, Møller discusses a vector form of the general Lorentz transformations, including the transformation:
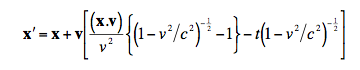
How did Møller get this expression? To do so, he first used ordinary Cartesian coordinate algebra, by itself, to obtain the Lorentz transformations, including:
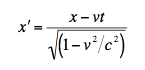
for the common, special case in which the coordinate axes are aligned along the direction of relative displacement of the coordinate axes, as suggested by Goenner. The important point to notice is that in the five pages that Møller used to derive the special Lorentz transformations, he (like Einstein) did not use the kinematic vectorial distinctions between velocity and speed, and between displacement, distance, position. In fact, he only uses the words ‘velocity,’ ‘distance’ and ‘coordinate.’ Hence, Møller does not actually derive the Lorentz transformations from kinematic vector concepts, instead he just rewrites the coordinate version in terms of vectors.
Instead, I want to see a derivation of the Lorentz transformations that solely uses kinematic vector concepts and vector algebra all throughout, systematically upholding distinctions between positions, distances, or displacements, and velocities or speeds. My impression is that any such efforts suffer of vector for scalar substitutions that cannot be done without writing expressions that exhibit the kind of pathologies I described in Kinematics, such as vector = scalar x scalar. Many or most coordinate derivations of the transformations involve steps in which something that was originally non-directional, such as a length x, suddenly becomes treated as directional or admitting negative values (as a position or displacement); v and c are inconsistently used as both speeds and velocities (ambiguities that are hardly solved with the operation of absolute value, because it has certain awkward operational consequences). Again, ordinary numbers, even when treated algebraically, simply lack the necessary vectorial distinctions, because in arithmetic 5 = +5, whereas in kinematics a distance of 5 is not equal to a displacement of +5. Also, a fundamental aspect of vector theory was the rule for the addition of vectors, and velocities are vectors; yet Einstein’s theory produced a new addition rule for velocities among systems in relative motion. There are also intrinsic problems concerning division of vectors, which is therefore often left undefined. Moreover, there are broader inconsistencies: since physicists had established that the Gibbs-Heaviside vector system is entirely equivalent to motions in a three-dimensional Euclidean space, how can one possibly derive a four-dimensional Minkowski spacetime from it? What I argued in Kinematics is that there is something more open or general in traditional “Cartesian” algebra that allows for such departures from 3-d Euclidean space. This is analogous to the way in which Cartesian algebra served to circumvent the difficulties in the foundations of Euclidean geometry, as noted for example by Hermann von Helmholtz; a non-obvious lack of one-to-one correspondence between analytic geometry and Euclidean geometry. Goenner disregards what I explain about vectors because he prefers to set things up as usual and he accepts the standard college sales pitch (originally by Gibbs) that the Gibbs-Heaviside vector algebra is exactly equivalent to coordinate algebra, but I explain in the book some of the kinematic problems with this claim.
Not everyone is as dismissive of my arguments about vectors as Goenner. For example, Jürgen Renn has remarked that this issue about vectors and algebraic notations “throws new light on this text [Einstein’s 1905 paper] that ironically has largely been passed over in silence by so many earlier scholars.” Likewise, Daniel Kennefick has argued that
“It is certainly interesting that, as Martínez argues in the book, Einstein did not make use of vectors in his work on relativity, but relied on purely algebraic methods, and there are interesting remarks even on Einstein’s idiosyncratic use of sign choices in his coordinate system. There seems to me something rather deep here surrounding the whole question of the role of vectors in the genesis of relativity theory which had not occurred to me before reading this book. If one simply reads Hamilton, with his quaternions, consisting of a scalar and a vector considered as one entity, and Minkowski, with his four-vectors, one could naturally leap to the conclusion that the two men did not require any intermediate work to invent relativity theory. But in fact physicists, as Martínez shows, had first to reject quaternions in favor of a purely vectorial approach, which was itself quite slow to catch on, and Einstein seems to have struggled through to his understanding of the basic kinematical need for relativity by decisively ignoring vectors and analyzing space and time in their kinematical aspects, as Ampère had done. For me this basic storyline is the narrative that emerged very strongly from the text, taking me somewhat by surprise and leaving me hungry for more.”
Regardless, Goenner further says that my statements “cast doubt on the scope of [my] knowledge in mathematics and physics.” Now certainly, I do not presume to know more physics and mathematics than Goenner, but let’s see the specific examples he gives. He continues: “for example, when time is conceived as a scalar (p. 401, including n. 74).” So what did I write on page 401? I wrote that: “Because t was conceived as a scalar, it would seem to be exempt from the directional distinctions inherent in the symbols for speed and velocity, and position, distance, or displacement.” Now, because this is a historical point, it is a non-interpretive matter of documentary fact whether vector theorists such as Gibbs and Heaviside in the 1890s conceived of time as a scalar. And of course, Goenner is plainly wrong. As I explained in my book, the concept of “scalar” was introduced by William Rowan Hamilton in a paper of 1844 in which he defined it specifically as referring to time, as a line without any direction in space. This notion was echoed extensively, by physicists and mathematicians in both general and definitive works. For example, all of the following very clearly defined or treated time as a scalar:
Josiah Willard Gibbs, Elements of Vector Analysis (1881).
Oliver Heaviside, “Elements of Vectorial Algebra and Analysis,” Electromagnetic Theory, Vol. 1 (1893), p. 177; and Electrical Papers, Vol. 2 (1892), p. 243.
Alexander Macfarlane, Principles of the Algebra of Physics (1894), p. 104.
Edward Nichols and William Franklin, The Elements of Physics (1896), Vol. 1, p. 19.
E. B. Wilson, Vector Analysis: a Text-Book for the Use of Students of Mathematics and Physics, based on lectures by J. W. Gibbs (1901), Chapter 1, p. 1, paragraph 1.
So, Goenner’s criticism is mistaken. Next, Goenner gives just one more example of my alleged confusions in mathematical physics, he complains that “the (real) [Goenner’s word] Coriolis force is called [in my book] ‘not actually a physical force but a descriptive formal by-product of the rotating reference frame.’ (p. 73 n. 15).” Again, this is an elementary point: when freely moving objects are viewed from a rotating reference frame they exhibit an apparent deflection, a relative acceleration that can be used in the rotating frame to describe a “force” named for Gaspard Gustav de Coriolis. In classical mechanics, to describe problems on the reference frame of our rotating Earth, physicists routinely use the Coriolis force and often call it “an inertial force,” “an apparent force,” “a fictitious force,” and “a pseudo force.” Among the four interactions or forces: electromagnetic, strong, weak, gravitational, I don’t know if Goenner wants to add a fifth, a “real Coriolis force” (which would be bizarre because the Coriolis force cannot be ascribed to any identifiable originating body), or if he is merely insinuating that Einstein’s principle of equivalence entitles him to view reference frame acceleration forces as equal to gravity. I stand by what I wrote, it is very commonplace, but I would be glad to see Goenner or anyone explain the contrary.
Next, Goenner further complains that my explanation of the “path to equations (E5) and (E6) takes three pages when in fact no calculation is needed at all.” He may well see such things as immediately obvious, but since Einstein’s actual paper of 1905, before presenting equation (E6), explicitly referred to “An analogous consideration [to his procedure for obtaining (E5)]” leads to (E6) “when we note that as observed from the resting system light always propagates along these axes with the speed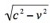 
,” then it is fair to explain how, applying the same considerations Einstein used for (E5), we can obtain (E6) as well. That’s what I did, and that’s also what Arthur I. Miller did, somewhat differently, in his analysis of Einstein’s 1905 paper in his book of 1981. I do not expect accounts of Einstein’s expressions to be lively or entertaining, but if readers wish to trace some of the implicit mathematical procedures I expect that my accounting of Einstein’s first derivation of the Lorentz transformation will be useful. Goenner disagrees, which is fine, I certainly don’t expect to please everyone.
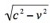,” then it is fair to explain how, applying the same considerations Einstein used for (E5), we can obtain (E6) as well. That’s what I did, and that’s also what Arthur I. Miller did, somewhat differently, in his analysis of Einstein’s 1905 paper in his book of 1981. I do not expect accounts of Einstein’s expressions to be lively or entertaining, but if readers wish to trace some of the implicit mathematical procedures I expect that my accounting of Einstein’s first derivation of the Lorentz transformation will be useful. Goenner disagrees, which is fine, I certainly don’t expect to please everyone. Moving on, Goenner admits that he “noticed only a few historical shortcomings.” He gives just two examples. First, he complains that I referred to a manuscript sketch of Einstein’s life written by his sister (1924), in which she noted that having published his relativity paper of 1905 Einstein received a letter from Max Planck asking him to clarify a few points. Goenner exclaims that “On the contrary, in his first contribution to special relativity, in 1906, Planck corrected a mistake made by Einstein!” But actually, Goenner’s reference to Planck’s well-known paper of 1906 is quite irrelevant to what I wrote, which is that Einstein received an early letter from Planck. We do not have that letter, to read what it said, because much of Einstein’s early correspondence is lost (he moved many times, and did not return to his home in Germany when Hitler came to power in 1933), and, because Planck’s papers where destroyed when the suburb of Grünewald along with his house was bombed in an air raid on 15 February 1944. Goenner can choose to disregard the account given by Einstein’s sister, but then he also has to disregard that Einstein’s son-in-law, Rudolf Kayser also reported that Einstein received an early letter from Planck (in a book that Einstein described as accurate), and he has to also disregard that Einstein himself, in a letter of 3 May 1906, remarked that “Prof. Planck (Berlin) wrote me about it recently.” As I explained above, we should not dismiss accounts simply because they are retrospective, what matters is the consistency of evidence. Someone might choose to imagine that Planck immediately and entirely understood Einstein’s arguments and therefore had no questions, but that would be an arbitrary act of the imagination, as to the contrary, many physicists had various difficulties coming to terms with Einstein’s work, and about Planck I simply conveyed a bit of available extant evidence.
Second, Goenner found an inconsequential slip in my book: a mention in a footnote that G.T. Fechner taught at Göttingen; Goenner is right, I mistakenly wrote Göttingen instead of Leipzig. Finally, Goenner ends his review by giving me a half compliment: “Although information is often repeated, the author’s writing guarantees pleasant reading.” Well, I hope that my comments on his review have been fine too.
Update:
Professor Goenner has kindly sent me an additional email, answering my question about vectors; he listed four books:
R. U. Sexl and H. K. Urbandtke, Relativitaet, Gruppen, Teilchen, 2nd ed. (Wien: Springer, 1982), pp. 116-120.
W. G. Dixon, Special Relativity (Cambridge: Cambridge University Press 1978), pp. 15-21.
J. Aharoni, The Special Theory of Relativity (New York: Dover 1965), pp. 49-50.
Henri Arzeliès, Relativitic Kinematics (Oxford: Pergamon Press, 1962).
In Kinematics, I wrote “Physicists did not merely neglect the use of vector algebra to formulate relativity theory; ordinary vector algebra could not be used to derive relativity theory.” (p.381)
I was explicitly referring to the vector algebra developed by Heaviside and Gibbs and the kinematic concepts elucidated by E.B. Wilson in 1901.
In Kinematics, I had used and cited Arzeliès’s excellent book, and he proceeds as Møller, above, so I have nothing to add. Likewise, I knew Aharoni’s book and neither does it provide the kind of derivation in question; instead, he begins by deriving the special Lorentz transformations by using coordinates, linear algebra, matrices and determinants, without using the vectorial kinematic distinctions I specified. Aharoni next rotates the coordinate axes to be no longer parallel, using trigonometry to express the more general transformations, and afterward, he immediately rewrites them in vector notation, like Møller, having still not used the kinematic concepts in question.
Now, Dixon (1978) uses column vectors (matrices) to derive the LT in a four-dimensional space, by beginning from projectivity:
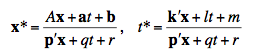
These general transformations preserve uniform rectilinear motions, but their use from the outset leaves me unsatisfied too because they are not explicitly derived from kinematic vector and scalar concepts: velocities, speeds, positions, displacements, distances, and clock readings.
Now, before discussing Sexl and Urbantke’s textbook, let me first summarize some of the historical background. In 1843, Hamilton formulated quaternions (with the new imaginary terms j, k) as what he intended to be a vector algebra ideally suited for the analysis of three-dimensional space. At the same time, Grassmann independently formulated a theory of extension applicable to spaces of many dimensions. In quaternions, to interpret the fourth term (a scalar), Hamilton sometimes entertained the idea that it might represent a fourth dimension. Meanwhile, Cayley complained that although quaternions are useful in two-dimensional geometry, they do not really show up in operations on three-dimensional geometry. Nevertheless, Tait emphasized the superiority of quaternions by arguing that they alone are uniquely suited for the analysis of three-dimensional Euclidean space. Unconvinced, Gibbs and Heaviside eliminated the fourth term from quaternions, so that they could formulate a vector algebra better suited for the analysis of physical problems in three-dimensional space. Gibbs and Heaviside also eliminated the imaginary components of Hamilton’s vectors. Gibbs appreciated Grassmann’s approach more than Hamilton’s quaternions because Grassmann’s system could be applied to spaces of four or more dimensions, yet the vector algebra of Gibbs was designed essentially for three-dimensional Euclidean space. In any case, the algebras of quaternions and vectors deviated from traditional algebra partly because they violated some of its traditional laws. Next, by 1901 E.B. Wilson had elucidated Gibbs’s algebra in detail, including systematic distinctions between scalar and vectorial kinematic concepts. In 1905, and for decades thereafter, Einstein formulated and reformulated the special theory of relativity in terms of traditional coordinate algebra, not using the notations, operations, or kinematic concepts of early vector theory. In this regard, I argued that if we try to convert Einstein’s derivations of the LT into kinematic vector concepts, there are certain steps that cannot be carried out. Here’s an example that I discussed in the book: In vector kinematics we must have x = ct and -x = -ct (i.e., the opposite of a displacement is the opposite of that displacement), but instead, Einstein used coordinate expressions such as: ξ = cτ, η = cτ, ζ = cτ, in order to derive the LT, as well as: x = ct and –x = ct, simultaneously (such equations seem to say that different positions are all equal to the same distance). Traditional “Cartesian” coordinate algebra therefore seems more accommodating than the narrow and specific vector algebra of Gibbs, Heaviside and Wilson because coordinate algebra can be used to formulate Euclidean, Minkowski, and non-Euclidean geometries. Minkowski disliked quaternions as narrow and clumsy for the analysis of four dimensions, so he instead reformulated special relativity analytically (by way of Cayley’s matrix methods) in terms of a four-dimensional manifold using Poincaré’s imaginary time coordinate as its fourth dimension.
Consequently, physicists extended the concepts and methods of vectors, amalgamated with the mathematics of matrices, to formulate other four-dimensional accounts of Einstein’s special theory. In particular, in 1910, Gilbert N. Lewis published a paper proposing to use vector methods instead of Minkowski’s matrices to formulate relativistic kinematics. To do so, he noted that “our present vector analysis” had not been used for that purpose because of its “restricted and specialized character,” as I’ve argued, and thus he proposed to articulate necessary modifications in order to make it applicable to spaces of four and higher dimensions. Lewis required the following departures from ordinary vector analysis: distinctions between vectors of different orders, reversing the meaning of the outer and inner products of a and b x c, generalizing common vector relations, and hence he explained how to develop what he called “a Euclidean four-dimensional space,” including the axis ict. Also in 1910, Sommerfeld developed Minkowski’s ideas by formulating a four-dimensional vector algebra and analysis for relativity (but mostly by the mere juxtaposition of coordinates, not by using as many vector operations and concepts). Furthermore, A. Conway and L. Silberstein used instead Hamilton’s quaternions to reformulate STR. What matters for my argument is that, just as in the work of Lewis, E.B. Wilson too, though having helped to definitively articulate Gibbs’s vector theory, did not then merely apply it to relativity. Instead, Wilson argued that relativity theory required what he called a “four dimensional non-Euclidean geometry” and proceeded to develop that new vector theory with the help of Lewis, publishing their approach in 1912. To that end, Gibbs and Lewis renounced the use of an imaginary coordinate and introduced a set of geometric postulates for rotation transformations absent in Euclidean geometry (e.g., that given a center of rotation there is not one but two lines through that point that remain unchanged in rotation). They also argued that, by contrast to Euclidean geometry, the inner product of a vector by itself is not always positive, and that outer products are all not merely scalars because in higher dimensions they exhibit a certain dimensionality; and so forth. Likewise, when attempting to apply ordinary vector algebra to hyperbolic space, V. Varičak found insurmountable difficulties.
So, consider now the derivation by Sexl and Urbantke (rev. ed. 2001). They prefer to base most of their derivation on the principle of relativity, the finiteness postulate, group theory, exclusion of time reversal, and in particular, leaving the light postulate for the end. Distinguishing between vectors and scalars, Sexl and Urbantke derive general transformations that work for theories involving a principle of relativity:
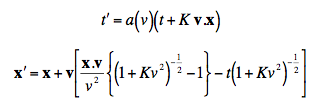
I’ve changed their notation to match Møller’s, above. By setting K = 0 and a = +1, we obtain Galilean transformations. Sexl and Urbantke thus show how close we get to the form of the special relativistic transformations, without using the light postulate. Next, how do they reach the Lorentz transformations? It is at this point that, if my claim were mistaken, we should encounter scalar and vector distinctions among the kinematic concepts I specified. So, to find the value of K, Sexl and Urbantke require the identity:
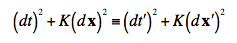
“where K has the physical dimension of reciprocal velocity squared.” They then define the “invariant speed”
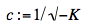
and we therefore have:
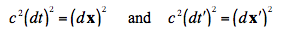
The identical use of K and c for both inertial systems, and for any directions, is just what I noted in Einstein’s derivations, and these steps depart from the Gibbs-Heaviside-Wilson system. And as I noted in my book (p.382), “Writers do not derive the vector formulation of the Lorentz transformations solely from vector concepts,” in the present case they used matrices, group theory, infinitesimals. Anyhow, by contrast to a Euclidean four dimensional space, the invariant squared interval (the quadratic form of coordinate differentials) in Minkowski space is not positive definite, thus excluding any real coordinate transformations that preserve this interval.
Summing up, the “vector theory” that is nowadays used to derive the Lorentz transformations is not identical with the early “vector theory” of Gibbs, Heaviside, Wilson. Moreover, some physicists such as Lewis and Gibbs were aware of intrinsic reasons why that early vector theory could not be used to derive the four-dimensional spacetime of Einstein’s kinematics. Still, looking back at Goenner’s criticism, I can see how my sentence on p.381, taken by itself, is not sufficiently specific, so it could be misunderstood as saying that no vectorial theories can possibly be used to derive Lorentz transformations. But then again, sentences should be read in context: just as my expression “relativity theory” in that same sentence on p.381 clearly refers to Einstein’s special theory, so too that page and chapter repeatedly specify early vector theory. Whereas, on p.383, I noted, of course, that “After the works of Poincaré and Einstein, theorists reformulated relativistic kinematics in terms of ‘four-dimensional vectors.’ This work was impelled by Minkowski...,” and so forth.
References
J. Aharoni, The Special Theory of Relativity (New York: Dover 1965).
Henri Arzeliès, Relativitic Kinematics (Oxford: Pergamon Press, 1962).
Arthur Cayley, “Coordinates Versus Quaternions,” Proceedings of the Royal Society of Edinburgh 20 (1895), 271-275.
A. W. Conway, “On the Application of Quaternions to Some Recent Developments of Electrical theory,” Proceedings of the Royal Irish Academy, A 29 (1911).
A. W. Conway, “The quaternionic form of relativity,” Philosophical Magazine, Series 6, 24 (1912), 790-809.
W. G. Dixon, Special Relativity (Cambridge: Cambridge University Press 1978), pp. 15-21.
Josiah Willard Gibbs, Elements of Vector Analysis (New Haven, 1881).
Hermann Grassmann, Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik… (Leipzig: Otto Wigand, 1844; and revised, expanded ed. Berlin: Adolph Enslin, 1862).
W. R. Hamilton, Lectures on Quaternions (Dublin: Hodges and Smith, 1853).
W. R. Hamilton, Elements of Quaternions (1866); Third edition, Vol. 1, edited by Charles Jasper Joly (New York: Chelsea Publishing Company, 1969).
Heaviside, Electromagnetic Theory, Vol. 1, Chapter III: “The Elements of Vectorial Algebra and Analysis” (London: Benn Brothers Ltd., The Electrician Printing and Publishing Company, 1894).
Gilbert N. Lewis, “On Four Dimensional Vector Analysis, and its Application in Electrical Theory,” Proceedings of the American Academy of Arts and Sciences 46, No. 7 (October 1910), 165-181.
Alberto A. Martínez, Kinematics: The Lost Origins of Einstein’s Relativity (Baltimore: Johns Hopkins University Press, 2009).
Arthur I. Miller, Albert Einstein’s Special Theory of Relativity: Emergence (1905) and Early Interpretation (1905-1911) (Reading, Mass.: Addison-Wesley, 1981); reprinted (New York: Springer Verlag, 1998).
Hermann Minkowski, “Raum und Zeit,” lecture delivered at the 80th Naturforscher-Versammlung at Köln on 21 September 1908; published in Physikalische Zeitschrift 10 (1909), 104-111.
Hermann Minkowski, “Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern,” Nachrichten der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-physikalische Klasse (1908), 53-111.
Christian Møller, The Special Theory of Relativity (Oxford: Clarendon Press, 1952).
Bertrand Russell, The Principles of Mathematics (1903); Second edition (New York: W. W. Norton & Company, Inc., 1938), article 219, p. 229.
Roman U. Sexl and Helmuth K. Urbantke, Relativity, Groups, Particles (New York: Springer, 2001), 1-9.
L. Silberstein, “Quaternionic form of relativity,” Philosophical Magazine 23 (1912), 790-809.
Arnold Sommerfeld, “Zur Relativitätstheorie, I. Vierdimensionale Vektoralgebra,” Annalen der Physik, series 4, 32 (1910), 749-776; “II. Vierdimensionale Vektoranalysis,” Annalen der Physik (4) 33 (1910), 649-689.
John Stachel, “‘What Song the Syrens Sang’: How Did Einstein Discover Special Relativity?” (1989), Einstein from ‘B’ to ‘Z’ (Boston: Birkhäuser, 2002).
P. G. Tait, “On the Importance of Quaternions in Physics,” Philosophical Magazine (January 1890); and, “On the Intrinsic Nature of the Quaternion Method,” Proceedings of the Royal Society of Edinburgh (2 July 1894).
Vladimir Varičak, Darstellung der Relativitätstheorie im dreidimensionalen Lobatchefskijschen Raume (Zagreb: Zaklada, 1924).
Scott Walter, “The Non-Euclidean Style of Minkowskian Relativity,” in J. Gray, ed., The Symbolic Universe (Oxford: Oxford University Press, 1999), 91–127.
E. B. Wilson, Vector Analysis: A Text-Book for the Use of Students of Mathematics and Physics, founded upon the Lectures of J. Willard Gibbs (New Haven: Yale University Press, 1901).
Edwin B. Wilson, and Gilbert N. Lewis, “The Space-Time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics,” Proceedings of the American Academy of Arts and Sciences 48, No. 10 (September 1912), 389-507.
